Next: (Przeciw)obrazy, ciągi Up: Wstęp do matematyki Previous: Relacje porządku
Partycją (podziałem) zbioru ![]() nazywamy każdą
rodzinę niepustych, parami rozłącznych podzbiorów zbioru
nazywamy każdą
rodzinę niepustych, parami rozłącznych podzbiorów zbioru ![]() ,
pokrywających w sumie cały zbiór
,
pokrywających w sumie cały zbiór ![]() 9.1. Innymi słowy, zbiór
9.1. Innymi słowy, zbiór
![]() nazywamy partycją zbioru
nazywamy partycją zbioru ![]() , gdy:
, gdy:
(a) każdy zbiór ![]() jest niepusty, tzn.
jest niepusty, tzn.
![]() ,
,
(b) różne zbiory
![]() są rozłączne, tzn.
są rozłączne, tzn.
![]() oraz
oraz
(c) każdy element ![]() należy do jakiegoś
należy do jakiegoś ![]() , tzn.
, tzn.
![]() .
.
Z każdą partycją ![]() zbioru
zbioru ![]() wiążemy pewną relację
wiążemy pewną relację ![]() na
zbiorze
na
zbiorze ![]() określoną następująco:
określoną następująco:
Przykład 0. Niech
![]() . Podział
zbioru
. Podział
zbioru ![]() na zbiory
na zbiory
![]() i
i
![]() to przykład partycji
to przykład partycji
![]() . Partycja ta ma trzy elementy. W
szczególności,
. Partycja ta ma trzy elementy. W
szczególności,
![]() oraz
oraz
![]() , jednak
, jednak
![]() . W tym przykładzie możemy łatwo wypisać wszystkie
elementy relacji
. W tym przykładzie możemy łatwo wypisać wszystkie
elementy relacji ![]() :
:
Przykład 1. Niech
![]() . Dla
. Dla
![]() niech
niech
![]() . Zatem
. Zatem
![]() jest partycją płaszczyzny
jest partycją płaszczyzny ![]() na proste równoległe do osi
na proste równoległe do osi ![]() . Relacja
. Relacja ![]() na zbiorze
na zbiorze
![]() odpowiadająca tej
partycji ma tu proste określenie: dla
odpowiadająca tej
partycji ma tu proste określenie: dla
![]() mamy
mamy
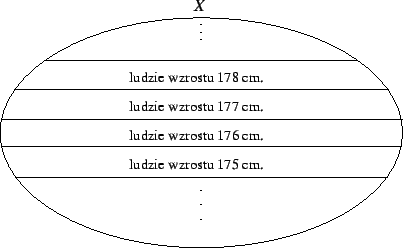
Przykład 2. Załóżmy, że ![]() oznacza zbiór ludzi. Możemy
próbować klasyfikować ludzi według pewnej cechy, na przykład
według wzrostu wyrażonego w centymetrach (w zaokrągleniu do
najbliższej liczby calkowitej). Dla
oznacza zbiór ludzi. Możemy
próbować klasyfikować ludzi według pewnej cechy, na przykład
według wzrostu wyrażonego w centymetrach (w zaokrągleniu do
najbliższej liczby calkowitej). Dla
![]() niech
niech
Z drugiej strony zbiór ![]() rozpada się tu na
rozłączne podzbiory złożone z ludzi tego samego wzrostu: elementy
partycji
rozpada się tu na
rozłączne podzbiory złożone z ludzi tego samego wzrostu: elementy
partycji ![]() . W każdym
z takich podzbiorów każde dwie osoby są względem siebie w relacji
. W każdym
z takich podzbiorów każde dwie osoby są względem siebie w relacji
![]() , osoby z różnych grup nie są względem siebie w relacji.
, osoby z różnych grup nie są względem siebie w relacji.
Przykład 3. Relacja równości ![]() na zbiorze
na zbiorze ![]() .
.
Przykład 4. Relacja równoległości
![]() na
zbiorze prostych na płaszczyźnie.
na
zbiorze prostych na płaszczyźnie.
Przykład 5. Relacja
![]() na zbiorze liczb całkowitych.
na zbiorze liczb całkowitych.
Przykład 6. Relacja ``
![]() i
i ![]() mają tych
samych rodziców'' na zbiorze ludzi.
mają tych
samych rodziców'' na zbiorze ludzi.
Przykład 7. Niech
![]() . Relacja
. Relacja ![]() na
na ![]() określona przez
określona przez
Relacje równoważności często oznaczamy symbolami podobnymi do ![]() ,
takimi jak na przykład
,
takimi jak na przykład
![]() .
Załóżmy teraz, że
.
Załóżmy teraz, że ![]() jest relacją równoważności na zbiorze
jest relacją równoważności na zbiorze
![]() . Elementy
. Elementy ![]() takie, że
takie, że ![]() nazywamy równoważnymi
(w sensie relacji
nazywamy równoważnymi
(w sensie relacji ![]() ). Na mocy symetryczności znaczy to również,
że
). Na mocy symetryczności znaczy to również,
że ![]() . Dla dowolnego
. Dla dowolnego ![]() definiujemy zbiór
definiujemy zbiór
Klasy abstrakcji relacji ![]() na zbiorze
na zbiorze ![]() to po prostu
zbiory-elementy partycji
to po prostu
zbiory-elementy partycji ![]() . Okazuje się, że klasy abstrakcji
dowolnej relacji równoważności tworzą partycję.
. Okazuje się, że klasy abstrakcji
dowolnej relacji równoważności tworzą partycję.
2. Jeśli ![]() , to
, to
![]() . By tego dowieść
najpierw pokażemy, że
. By tego dowieść
najpierw pokażemy, że
![]() . W tym celu
załóżmy, że
. W tym celu
załóżmy, że
![]() , tzn.
, tzn. ![]() . Wtedy z
. Wtedy z ![]() i
przechodniości dostajemy
i
przechodniości dostajemy ![]() , czyli
, czyli
![]() . Podobnie pokazujemy, że
. Podobnie pokazujemy, że
![]() .
.
3. Jeśli ![]() (tzn.
(tzn. ![]() ), to
), to
![]() . Tu prowadzimy dowód nie
wprost. Przypuśćmy, że pewne
. Tu prowadzimy dowód nie
wprost. Przypuśćmy, że pewne
![]() . Wtedy
(na mocy definicji klasy abstrakcji i symetryczności
. Wtedy
(na mocy definicji klasy abstrakcji i symetryczności ![]() ):
):
![]() i
i ![]() , więc z przechodniości
, więc z przechodniości ![]() ,
sprzeczność.
,
sprzeczność.
Stąd dostajemy, że różne zbiory należące do ![]() są parami rozłączne,
tzn. jeśli
są parami rozłączne,
tzn. jeśli
![]() , to
, to
![]() . Istotnie, rozumujemy tu nie
wprost. Przypuśćmy, że
. Istotnie, rozumujemy tu nie
wprost. Przypuśćmy, że
![]() . Na
mocy 3. i prawa transpozycji dostajemy stąd
. Na
mocy 3. i prawa transpozycji dostajemy stąd ![]() , czyli (na mocy
2.)
, czyli (na mocy
2.)
![]() .
. ![]()
Zasada abstrakcji. W przykładzie 2. podział zbioru ludzi na klasy abstrakcji odbywał
się według znanej cechy: wzrostu. Załóżmy, że ![]() jest relacją
równoważności na zbiorze
jest relacją
równoważności na zbiorze ![]() . Możemy traktować klasę abstrakcji elementu
. Możemy traktować klasę abstrakcji elementu
![]() jako nowy obiekt, swoistą cechę
elementu
jako nowy obiekt, swoistą cechę
elementu ![]() wspólną dla wszystkich elementów w tej samej klasie
abstrakcji (w przykładzie 0. tą cechą był wzrost). Zasada
abstrakcji polega własnie na definiowaniu w ten sposób nowych
pojęć, nowych własności różnych obiektów.
wspólną dla wszystkich elementów w tej samej klasie
abstrakcji (w przykładzie 0. tą cechą był wzrost). Zasada
abstrakcji polega własnie na definiowaniu w ten sposób nowych
pojęć, nowych własności różnych obiektów.
W ten sposób
definiuje się na przykład kierunek prostej ![]() na
płaszczyźnie: jest to klasa abstrakcji prostej
na
płaszczyźnie: jest to klasa abstrakcji prostej ![]() względem relacji równoległości
prostych z przykładu 4, czyli wspólna cecha klasy prostych równoległych. Opis klas abstrakcji relacji z pozostałych
przykładów pozostawiamy jako ćwiczenie.
względem relacji równoległości
prostych z przykładu 4, czyli wspólna cecha klasy prostych równoległych. Opis klas abstrakcji relacji z pozostałych
przykładów pozostawiamy jako ćwiczenie.
Rodzina klas abstrakcji wyznacza
relację równoważności, podobnie jak tabelka wartości logicznych
wyznacza spójnik logiczny. W rachunku zdań określaliśmy wręcz
nowe abstrakcyjne spójniki logiczne zadając dowolnie ich tabelki
wartości.
Teraz sytuacja jest podobna: wychodząc od dowolnego podziału ![]() zbioru
zbioru
![]() na zbiory rozłączne i niepuste dostajemy relację
równoważności
na zbiory rozłączne i niepuste dostajemy relację
równoważności ![]() , której klasami abstrakcji są dokładnie te zbiory.
, której klasami abstrakcji są dokładnie te zbiory.
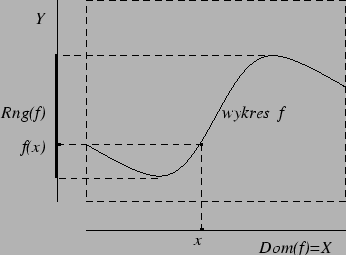
Funkcje. Jeśli każdemu elementowi ![]() zbioru
zbioru ![]() przypisany jest
jeden element
przypisany jest
jeden element ![]() zbioru
zbioru ![]() (niekoniecznie ten sam dla różnych
elementów
(niekoniecznie ten sam dla różnych
elementów ![]() ), to mówimy, że na zbiorze
), to mówimy, że na zbiorze ![]() określona
jest funkcja (inaczej: przekształcenie lub odwzorowanie) przekształcająca zbiór
określona
jest funkcja (inaczej: przekształcenie lub odwzorowanie) przekształcająca zbiór ![]() w zbiór
w zbiór ![]() , zaś
, zaś ![]() jest
wartością tej funkcji dla argumentu
jest
wartością tej funkcji dla argumentu ![]() . Oznaczając taką funkcję
przez
. Oznaczając taką funkcję
przez ![]() , piszemy wtedy
, piszemy wtedy
Innymi słowy, funkcja ![]() jest to dowolna relacja
jest to dowolna relacja ![]() między elementami zbioru
między elementami zbioru ![]() a elementami zbioru
a elementami zbioru ![]() , której dziedzina to cały zbiór
, której dziedzina to cały zbiór ![]() , taka
że dla każdego
, taka
że dla każdego ![]() istnieje dokładnie jeden
istnieje dokładnie jeden ![]() taki, że
taki, że
![]() .
Z tego względu, gdy zbiory
.
Z tego względu, gdy zbiory ![]() i
i ![]() są skończone, możemy przedstawić funkcję
są skończone, możemy przedstawić funkcję ![]() w postaci
diagramu. Strzałka od
w postaci
diagramu. Strzałka od ![]() do
do ![]() oznacza, że
oznacza, że ![]() .
.
Przykład 0. Funkcja zdaniowa
![]() , to funkcja
przypisująca elementom
, to funkcja
przypisująca elementom ![]() zbioru
zbioru ![]() zdania
zdania ![]() .
.
Przykład 1. Funkcja pusta
![]() ,
dziedziną i obrazem tej funkcji jest również zbiór pusty.
,
dziedziną i obrazem tej funkcji jest również zbiór pusty.
Przykład 2. Dla dowolnego zbioru ![]() funkcja identycznościowa
funkcja identycznościowa
![]() dana jest wzorem
dana jest wzorem ![]() . Funkcja stała to
funkcja, która dla wszystkich argumentów przyjmuje tę samą stałą
wartość.
. Funkcja stała to
funkcja, która dla wszystkich argumentów przyjmuje tę samą stałą
wartość.
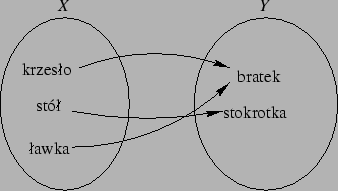
Przykład 3. Niech ![]() krzesło, stół, ławka
krzesło, stół, ławka![]() bratek,
stokrotka
bratek,
stokrotka![]() . By określić funkcję
. By określić funkcję
![]() wystarczy
wypisać jej wartości dla wszystkich argumentów. Zamiast tego można
też narysować jej diagram. Przykładowo możemy określić
wystarczy
wypisać jej wartości dla wszystkich argumentów. Zamiast tego można
też narysować jej diagram. Przykładowo możemy określić ![]() przez
zdefiniowanie:
przez
zdefiniowanie:
Diagram tak określonej funkcjikrzesło
bratek,
stół
stokrotka i
ławka
bratek.
Przykład 4. Funkcje
![]() i
i
![]() określone wzorami
określone wzorami
Z każdą funkcją ![]() związana jest pewna relacja
związana jest pewna relacja ![]() na
zbiorze
na
zbiorze ![]() określona wzorem
określona wzorem
(2) ![]() jest ``na'' (inaczej: jest surjekcją), gdy cały zbiór
jest ``na'' (inaczej: jest surjekcją), gdy cały zbiór ![]() jest
zbiorem wartości
jest
zbiorem wartości ![]() . Symbolicznie:
. Symbolicznie:
Przykład 1.
![]() dana jest wzorem
dana jest wzorem ![]() . Wówczas
. Wówczas ![]() jest ``na'', jednak nie
jest 1-1, bo np.
jest ``na'', jednak nie
jest 1-1, bo np. ![]() .
.
Przykład 2.
![]() określona jest wzorem
określona jest wzorem
(2) ![]() jest ``na''. Niech
jest ``na''. Niech ![]() oraz
oraz ![]() . Widzimy, że
. Widzimy, że
![]() i
i ![]() . Dlatego
. Dlatego
![]() , czyli
, czyli
![]() .
.
(3) ![]() jest odwrotna do
jest odwrotna do ![]() , gdyż mamy
, gdyż mamy
![]() .
. ![]()
Przykład.
![]() dana jest wzorem
dana jest wzorem
![]() . Zatem jest to bijekcja. Wzór na funkcję odwrotną
znajdujemy następująco. Mamy następujący ciąg równoważnych
funkcji zdaniowych zmiennych
. Zatem jest to bijekcja. Wzór na funkcję odwrotną
znajdujemy następująco. Mamy następujący ciąg równoważnych
funkcji zdaniowych zmiennych
![]() :
:
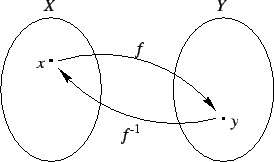
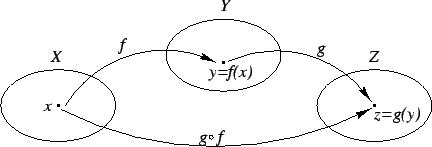
Składanie funkcji. Załóżmy, że ![]() oraz
oraz ![]() . Wtedy definiujemy funkcję
. Wtedy definiujemy funkcję
![]() wzorem
wzorem
![]() . Prawa strona tego wzoru ma sens, bo dla
. Prawa strona tego wzoru ma sens, bo dla
![]() oraz
oraz ![]() jest dziedziną
jest dziedziną ![]() , więc
, więc ![]() istnieje.
Funkcję
istnieje.
Funkcję ![]() nazywamy złożeniem (lub superpozycją) funkcji
nazywamy złożeniem (lub superpozycją) funkcji
![]() i
i ![]() . Piszemy też
. Piszemy też ![]() zamiast
zamiast ![]() .
.
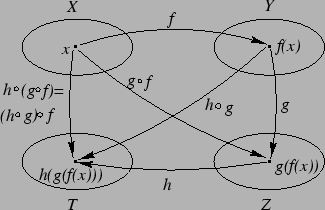
Dla ![]() możemy wykonywać wielokrotną superpozycję
możemy wykonywać wielokrotną superpozycję ![]() z
sobą. Dla
z
sobą. Dla ![]() przyjmujemy oznaczenia:
przyjmujemy oznaczenia:
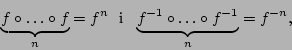
Obcinanie (ograniczanie) i rozszerzanie funkcji.
Załóżmy, że ![]() ,
, ![]() oraz
oraz
![]() .
.
(1) Definiujemy funkcję
![]() . Dla argumentów
. Dla argumentów ![]() wartości
wartości ![]() są te same, co wartości
są te same, co wartości ![]() ,
tzn.
,
tzn.
![]() . Funkcję tę nazywamy obcięciem
(ograniczeniem) funkcji
. Funkcję tę nazywamy obcięciem
(ograniczeniem) funkcji ![]() do zbioru
do zbioru ![]() .
.
(2) Funkcję ![]() nazywamy rozszerzeniem funkcji
nazywamy rozszerzeniem funkcji
![]() dla każdego
dla każdego ![]() mamy
mamy ![]() (innymi
słowy, gdy
(innymi
słowy, gdy ![]() jest obcięciem funkcji
jest obcięciem funkcji ![]() do
do ![]() ).
).
Załóżmy teraz, że
![]() . Wartość
. Wartość
![]() funkcji
funkcji ![]() dla
dla
![]() zapisujemy w
postaci
zapisujemy w
postaci
![]() . Funkcję
. Funkcję ![]() nazywamy wtedy
nazywamy wtedy ![]() -argumentową, zaś elementy
-argumentową, zaś elementy
![]() nazywamy argumentami funkcji
nazywamy argumentami funkcji ![]() .
.
Ludomir Newelski 2006-08-29