Indukcja matematyczna

Indukcja polega na wyciąganiu ogólnych wniosków na podstawie skończenie wielu przypadków. Przykładowo wielekroć obserwowaliśmy, że jabłko puszczone z pewnej wysokości spada. Newton wywnioskował stąd ogólne prawo ciążenia. Podobnie obserwując codzienne wschody słońca można po pewnym czasie dojść do przekonania, że słońce zawsze wschodzi o świcie. Jak wiemy, w długim okresie czasu nie będzie to jednak prawda. Zatem metoda indukcji jest zawodną metodą wnioskowania.

Podobnie w matematyce można obserwować, że pewne własności liczb naturalnych przysługują kolejno liczbom $0,1,2,3,4,5,\dots$ Po sprawdzeniu wielu takich liczb pojawia sie pokusa, by metodą indukcji przyjąć, że dana własność przysługuje wszystkim liczbom naturalnym. Droga ta prowadzić może na manowce.

Przykład. Niech $a_0=0,a_1=14,a_2=128,a_3=1170,a_4=10695,a_5=97763,$ zaś dla $n\geq 1$

$$a_{n+5}=10a_{n+4}-8a_{n+3}+a_{n+2}+3a_{n+1}+2a_n.$$

Ponadto niech $b_0=0, b_1=14, b_2=128$, zaś dla $n\geq 1$

$$b_{n+2}=\left[{b_{n+1}^2\over b_n}+{1\over 2}\right],$$

nawias kwadratowy oznacza tu część całkowitą liczby rzeczywistej. Wtedy $a_n=b_n$ dla $n\leq 5015$ oraz $a_{5016}\neq b_{5016}$.^13.1

W odróżnieniu od zawodnej metody indukcji opisanej powyżej, indukcja matematyczna jest jak najbardziej niezawodną metodą dowodzenia twierdzeń. Nazwa tej metody bierze się z pewnego zewnętrznego podobieństwa do metody indukcji.

Indukcja matematyczna dotyczy własności liczb naturalnych. W rozdziale 11 podaliśmy, jak w teorii mnogości definiuje się liczby naturalne. Przypomnijmy, że $0$ to zbiór pusty $\emptyset$, zaś liczba $n+1$ to zbiór $n\cup\{n\}$. W teorii mnogości definiuje się zbiór liczb naturalnych $\mathbb{N}$ jako najmniejszy zbiór $Z$ taki, że

1. $0\in Z$ i
2. dla każdego $n\in Z$ mamy $n\cup\{n\}\in Z$.

Istnienie takiego zbioru $\mathbb{N}$ przyjmuje się w teorii mnogości w zasadzie jako aksjomat. Z tej definicji wynika natychmiast następująca zasada.

Twierdzenie 13..1 (Zasada indukcji matematycznej)   Jeśli $Z$ jest podzbiorem zbioru liczb naturalnych $\mathbb{N}$ takim, że

1. $0\in Z$ i
2. dla każdego $n\in Z$ mamy też $n+1\in Z$,

to wtedy $Z$ jest zbiorem wszystkich liczb naturalnych.

Dowód. Jeśli $Z$ spełnia warunki 1. i 2., to spełnia też warunki definiujące w teorii mnogości zbiór liczb naturalnych, więc ${\mathbb{N}}\subseteq Z$. Z założenia jednak $Z\subseteq\mathbb{N}$, więc $Z=\mathbb{N}$. $\Box$

Zasadę indukcji matematycznej formułuje się również w nieco innej postaci, w której można ją stosować bezpośrednio do dowodzenia twierdzeń. Mianowicie, dla każdej funkcji zdaniowej $\varphi(n),n\in\bf N$, jeżeli

1. $\varphi(0)$ i
2. dla każdego $n\in{\mathbb{N}}$, $\varphi(n)$ pociąga $\varphi(n+1)$,

to wtedy

3.

dla każdego $n\in\mathbb{N}$ mamy $\varphi(n)$.

Zasada indukcji matematycznej w tej formie wynika z twierdzenia 13.1, gdy za $Z$ przyjmiemy wykres funkcji zdaniowej $\varphi(n)$. Punkty 1. i 2. w tej zasadzie nazywamy krokami indukcyjnymi (w punkcie 1. często pomijamy tę nazwę). Zdanie $(\forall n\in{\mathbb{N}})\varphi(n)$ nazywamy tezą indukcyjną (tezą indukcyjną nazywa się też samą funkcję zdaniową $\varphi(n)$). Formalnie zasadę indukcji matematycznej dla funkcji zdaniowej $\varphi(n),n\in\mathbb{N}$ możemy zapisać w postaci zdania

$$\varphi(0)\land(\forall n\in N)(\varphi(n)\Rightarrow\varphi(n+1))\Rightarrow(\forall n\in{\bf N})\varphi(n).$$

Z zasady indukcji matematycznej wynika tak zwana zasada minimum.

Twierdzenie 13..2 (Zasada minimum)   Każdy niepusty podzbiór zbioru liczb naturalnych zawiera element najmniejszy.

Dowód. Niech $X$ będzie niepustym podzbiorem $\bf N$ i niech

$$Z=\{n\in{\mathbb{N}}: \{0,\dots,n\}\cap X=\emptyset\}.$$

Przypuśćmy nie wprost, że $X$ nie ma elementu najmniejszego. W szczególności $0\not\in X$ (bo $0$ jest najmniejszą liczbą naturalną), więc $0\in Z$.

Przypuśćmy teraz, że $n\in Z$. Znaczy to, że $\{0,\dots,n\}$ jest rozłączny z $X$. Jeśli teraz $n+1\in X$, to $n+1$ byłaby najmniejszą liczbą w $X$, sprzeczność. Dostajemy więc $n+1\not\in X$, czyli również $\{0,\dots,n+1\}\cap X=\emptyset$ i $n+1\in Z$.

W ten sposób widzimy, że zbiór $Z$ spełnia założenia twierdzenia 13.1. Dlatego wnioskujemy, że $Z=\mathbb{N}$. Znaczy to jednak, że $X=\emptyset$, sprzeczność. $\Box$

Przykład. Udowodnimy metodą indukcji matematycznej nierówność Bernoulliego: dla $x>-1$ i $n\geq 0$ mamy $(1+x)^n\geq 1+nx$.

Nasza teza indukcyjna to

$$(\forall n\in{\mathbb{N}})(\forall x>-1)(1+x)^n\geq 1+nx.$$

Zatem $\varphi(n)$ to funkcja zdaniowa $(\forall x>-1)(1+x)^n\geq 1+nx$.

1. Przypadek $n=0$ (sprawdzamy, że $\varphi(0)$). Niech $x>-1$.
$(1+x)^0=1\geq 1+0\cdot x$, więc $\varphi(0)$ zachodzi.

2. Krok indukcyjny. Przypuśćmy^13.2, że zachodzi $\varphi(n)$. Udowodnimy
$\varphi(n+1)$, tzn. $(\forall x>-1)(1+x)^{n+1}\geq 1+(n+1)x$.

Niech więc $x>-1$. Na mocy założenia indukcyjnego, $(1+x)^n\geq 1+nx$. Dlatego mamy

$$(1+x)^{n+1}=(1+x)^n(1+x)\geq (1+nx)(1+x)=1+(n+1)x+nx^2\geq 1+(n+1)x,$$

co kończy dowód kroku indukcyjnego.

Z zasady indukcji matematycznej wnioskujemy, że teza indukcyjna zachodzi dla wszystkich $n\in\mathbb{N}$.

Stosuje się też różne warianty zasady indukcji matematycznej.

Indukcja od miejsca $n_0\in \mathbb{N}$.

$$(*)\ \varphi(n_0)\land(\forall n\geq n_0)(\varphi(n)\Rightarrow\varphi(n+1))\Rightarrow(\forall n\geq n_0)\varphi(n)$$

Dowód. Wprowadzamy nową funkcję zdaniową $\psi(n),n\in\mathbb{N}$ wzorem

$$\psi(n)\Leftrightarrow\varphi(n+n_0).$$

Wtedy zdanie $(*)$ jest równoważne zdaniu

$$\psi(0)\land(\forall n\geq 0)(\psi(n)\Rightarrow\psi(n+1))\Rightarrow(\forall n\geq 0)\psi(n),$$

które wynika z zasady indukcji matematycznej.

Zasada indukcji porządkowej.

$$(\dagger)\ (\forall n\in{\mathbb{N}})((\forall k<n)\varphi(k)\Rightarrow\varphi(n))\Rightarrow(\forall n\in{\bf N})\varphi(n)$$

Przed dowodem zwróćmy uwagę, że ta forma indukcji ma tylko jeden krok indukcyjny:

$$(**)\ (\forall n\in{\mathbb{N}})((\forall k<n)\varphi(k)\Rightarrow\varphi(n)).$$

Jednak dla $n=0$ zdanie to mówi, że

$$(\forall k\in{\mathbb{N}})(k<0\Rightarrow\varphi(k))\Rightarrow\varphi(0).$$

Poprzednik tej implikacji, czyli zdanie

$$(\forall k\in{\mathbb{N}})(k<0\Rightarrow\varphi(k)),$$

jest prawdziwy (bo dla każdego $k\in\mathbb{N}$ $k<0$ jest fałszem), więc z $(**)$ wynika w szczególności, że $\varphi(0)$ jest prawdą. Zatem ``pierwszy krok'' indukcji jest tu jakby ukryty.
Dowód $(\dagger)$. Dowód przeprowadzimy przy użyciu zasady minimum. Przypuśćmy nie wprost, że $(**)$ zachodzi, jednak zbiór $X=\{n\in{\bf N}:\neg\varphi(n)\}$ jest niepusty. Niech $n_0$ będzie jego najmniejszym elementem. Wówczas prawdą jest, że $(\forall k<n_0)\varphi(k)$. Stosując $(**)$ dla $n=n_0$ dostajemy, że $\varphi(n_0)$, czyli $n_0\not\in X$, sprzeczność. $\Box$

Przykład. Udowodnimy, że liczba przekątnych $n$-kąta wypukłego jest równa $a_n={1\over 2}n(n-3)$.

Niech $\varphi(n),n\geq 3$ oznacza funkcję zdaniową: `` liczba przekątnych $n$-kąta wypukłego jest równa $a_n={1\over 2}n(n-3)$''. Wówczas nasza teza indukcyjna ma postać $(\forall n\geq 3)\varphi(n)$.

1. Sprawdzamy, że teza zachodzi dla $n=3$. Wówczas $a_3=0$ i jest to rzeczywiście liczba przekątnych trójkąta.

2. Krok indukcyjny. Przypuśćmy, że $n\geq 3$ oraz $\varphi(n)$ jest prawdziwe. Udowodnimy $\varphi(n+1)$.

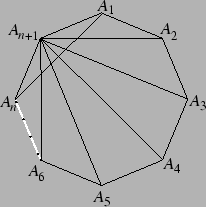
W tym celu rozważmy $(n+1)$-kąt wypukły $W$ o wierzchołkach $A_1,\dots A_{n+1}$. Wówczas $A_1,\dots,A_n$ są wierzchołkami $n$-kąta wypukłego $V$, który z założenia indukcyjnego ma $a_n={1\over 2}n(n-3)$ przekątnych.

Przekątne $W$ to dokładnie przekątne $V$ i dodatkowo $n-2$ przekątnych lączących $A_{n+1}$ z wierzchołkami $A_2,A_3,\dots,A_{n-1}$ oraz przekątna $A_1A_n$.

Łącznie liczba przekątnych $W$ wynosi

$${1\over 2}n(n-3)+(n-1)={1\over 2}[n(n-3)+2(n-1)]={1\over 2}(n+1)(n-2)=a_{n+1},$$

co kończy dowód.

Definicje rekurencyjne (indukcyjne).

Jeśli dana jest liczba $a\in\mathbb{N}$ i funkcja $f$ o dziedzinie ${\mathbb{N}}\times{\mathbb{N}}$, to możemy zdefiniować nową funkcję $h$ o dziedzinie $\mathbb{N}$ (czyli: ciąg), która spełnia następujący układ warunków

$$\left\{\begin{array}{lcl}h(0)&=&a\\ h(n+1)&=&f(n,h(n))\end{array}\right.$$

W definicji tej podajemy wartość funkcji $h$ dla argumentu $0$, a następnie wyznaczamy wartości $h$ dla kolejnych liczb naturalnych posługując się rekurencyjnym warunkiem $h(n+1)=f(n,h(n))$. W wariantach tej metody możemy określać wartości funkcji $h$ dla kilku początkowych argumentów, a następnie w warunku rekurencyjnym wartość $h(n)$ moze zależeć od wartości $h$ dla kilku poprzednich argumentów. W ten sposób definiujemy poniżej ciąg Fibonacciego. Używając zasady indukcji matematycznej można udowodnić, że w istocie istnieje jedyna funkcja $h$ określona tymi warunkami. Łatwiej jednak zrozumieć ten fakt na przykładzie.

Przykład. Ciąg Fibonacciego $(a_n)$ określony jest warunkami

$$\left\{\begin{array}{lcl}a_0&=&0\\ a_1&=&1\\ a_{n+2}&=&a_n+a_{n+1}\end{array}\right.$$

Mamy więc $a_0=0,a_1=1,a_2=a_0+a_1=1, a_3=a_1+a_2=2, a_4=a_2+a_3=3$ i tak dalej. Ogólnie można udowodnić (przez indukcję), że

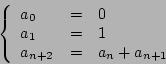
$$a_n={\sqrt{5}\over 10}\left[\left({1+\sqrt{5}\over 2}\right)^n-\left({1-\sqrt{5}\over 2}\right)^n\right].$$

Schemat definicji rekurencyjnej funkcji $2$ i więcej zmiennych wygląda podobnie. $n$ oznacza tu liczbę naturalną, zaś $f$ i $g$ są danymi funkcjami o odpowiednich dziedzinach. Wówczas definiujemy nową funkcje $h$ określoną warunkami

$$\left\{\begin{array}{lcl}h(x,0)&=&f(x)\\ h(x,n+1)&=&g(x,n,h(x,n))\end{array}\right.$$

Przykład. Niech $S:{\mathbb{N}}\to{\mathbb{N}}$ oznacza funkcję następnika, tzn. $S(n)=n+1$. Używając tej funkcji możemy zdefiniować rekurencyjnie dwuargumentowe funkcje dodawania i mnożenia liczb naturalnych.

$$\left\{\begin{array}{lcl}x+0&=&x\\ x+(n+1)&=&S(x+n) = (x+n)+1\end{array}\right.$$

$$\left\{\begin{array}{lcl}x\cdot 0&=&0\\ x\cdot(n+1)&=&(x\cdot n)+x\end{array}\right.$$

Podobnie definiujemy potęgowanie, tzn funkcję dwuargumentową $(x,n)\mapsto x^n$ dla $x>0$ i $n\in\mathbb{N}$.

ściśle rzecz biorąc, operacje $\sum_{k=0}^na_k$ i $\prod_{k=0}^na_k$ również są zdefiniowane rekurencyjnie (dla danego ciągu $(a_n)$).

$$\left\{\begin{array}{lcl} \medskip\sum_{k=0}^0a_k&=&0\\ \sum... ...k=0}^{n+1}a_k&=&\prod_{k=0}^na_k\cdot a_{n+1}\end{array}\right.$$

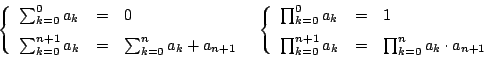
W wielu definicjach i rozumowaniach przeprowadzanych pozornie bez użycia indukcji tkwi ona jednak ukryta pod sformułowaniami typu ``i tak dalej'' lub napisami typu ``$\dots$''. Odnosi się to również często do sytuacji, gdzie zastępujemy dowód używający jawnie indukcji matematycznej przez dowód jakoby do tej zasady się nie odwołujący.