Next: Relacje porządku Up: Wstęp do matematyki Previous: Kwantyfikatory
W formule ![]() kwantyfikator
kwantyfikator ![]() odnosi się do formuły
odnosi się do formuły
Gdy w formule ![]() za symbole
za symbole ![]() i
i ![]() podstawimy konkretne
funkcje zdaniowe, stanie się ona sama (złożoną) funkcją zdaniową. Na
przykład, niech
podstawimy konkretne
funkcje zdaniowe, stanie się ona sama (złożoną) funkcją zdaniową. Na
przykład, niech ![]() oznacza funkcję zdaniową
oznacza funkcję zdaniową
![]() (tzn: ``
(tzn: ``![]() dzieli
dzieli ![]() ''), zaś
''), zaś ![]() oznacza
funkcję zdaniową
oznacza
funkcję zdaniową
![]() . Wówczas
. Wówczas ![]() staje się
funkcją zdaniową:
staje się
funkcją zdaniową:
dla każdej liczby naturalnejNie jest to prawda, gdyż np. liczba, jeśli
dzieli
, to
.
Można sprawdzić, że dla każdego
![]() , zdanie
, zdanie ![]() jest fałszywe, czyli
jest fałszywe, czyli
![]() .
.
Podobnie jak w rachunku zdań, wiele tautologii rachunku kwantyfikatorów ma postać równoważności. Pozwalają one przekształcać w sposób równoważny zdania tak, by uzyskać jak najprostszą formę.
zaśi
są równoważne.
ZdanieBy udowodnić równoważność obu zdań korzystamy z faktu, że zdaniejest prawdziwe.
![]() . Wystarczy udowodnić zdanie
. Wystarczy udowodnić zdanie ![]() zakładając, że
zakładając, że
![]() jest prawdziwe. Załóżmy, że
jest prawdziwe. Załóżmy, że ![]() jest prawdziwe, to znaczy
funkcje zdaniowe
jest prawdziwe, to znaczy
funkcje zdaniowe ![]() i
i ![]() są równoważne. Znaczy to,
że
są równoważne. Znaczy to,
że
![]() . Oznaczmy przez
. Oznaczmy przez ![]() ten zbiór.
Dlatego dla każdego
ten zbiór.
Dlatego dla każdego ![]() mamy, że zdania
mamy, że zdania ![]() i
i
![]() mają tę samą wartość logiczną (a mianowicie są oba
fałszywe, gdy
mają tę samą wartość logiczną (a mianowicie są oba
fałszywe, gdy ![]() i oba prawdziwe, gdy
i oba prawdziwe, gdy ![]() ).
Dlatego dla każdego
).
Dlatego dla każdego ![]() zdanie
zdanie
![]() jest prawdziwe. Oznacza
to, że
prawdziwe jest zdanie
jest prawdziwe. Oznacza
to, że
prawdziwe jest zdanie
![]() , czyli
, czyli ![]() .
.
![]() . Tu dowód pozostawiamy jako
ćwiczenie.
. Tu dowód pozostawiamy jako
ćwiczenie. ![]()
Podamy teraz przykłady prostych tautologii rachunku kwantyfikatorów. Wiele z nich ma postać równoważności.
(2) Obie strony równoważności mówią, że
![]() , dlatego są równoważne.
, dlatego są równoważne.
(4) Podobnie jak w punkcie (1) interpretujemy najpierw ![]() jako funkcję zdaniową na jakiejś (dowolnej) przestrzeni
jako funkcję zdaniową na jakiejś (dowolnej) przestrzeni
![]() . Mamy pokazać, że przy tej interpretacji zdanie
. Mamy pokazać, że przy tej interpretacji zdanie
Niech
![]() oznacza wykres funkcji zdaniowej
oznacza wykres funkcji zdaniowej
![]() . Zatem
. Zatem ![]() oznacza dokładnie, że
oznacza dokładnie, że
jeśli pewne cięcie pionowe zbioruBy to udowodnić, załóżmy, żejest całym
, to każde cięcie poziome zbioru
jest niepuste.
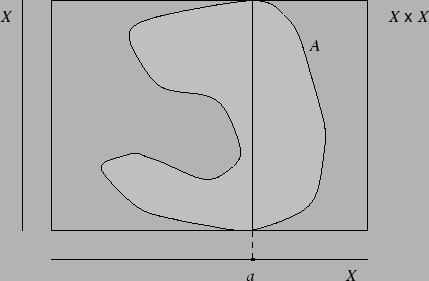
W tym miejscu zwróćmy uwage, że implikacja odwrotna do (4)
(5) Jak wyżej, rozważamy funkcje zdaniowe ![]() i
i
![]() . Mamy pokazać, że zdania
. Mamy pokazać, że zdania
Dowody pozostałych punktów jedną z powyższych metod pozostawiamy
jako ćwiczenie. ![]()
Należy tu zaznaczyć, że chociaż dowody, że powyższe formuły są tautologiami, są dość łatwe, ogólnie nie istnieje algorytm (tzn. przepis) sprawdzania, czy dana formuła jest tautologią. Jak pamiętamy, algorytm taki istnieje w przypadku tautologii rachunku zdań (tabelka).
Z uwagi na przemienność kwantyfikatorów stosujemy konwencję łączenia sąsiednich dużych
i sąsiednich małych kwantyfikatorów, tzn. zamiast
![]() piszemy
piszemy
![]() i podobnie dla
i podobnie dla
![]() .
.
Warto tu wspomnieć o tym, że niekiedy w matematyce traktuje się duży kwantyfikator jako kwantyfikator domyślny. Jest tak na przykład w zdaniach typu:
W przestrzeniOczywiście równośćprawdziwa jest równość
.
Aby uzasadnić, że formuła nie jest tautologią, trzeba podać przykład (tzn. interpretację tej formuły jako konkretnego zdania), w którym jest ona zdaniem fałszywym. W tym celu potrzebujemy dużo przykładów funkcji zdaniowych. Dostarczają ich nam relacje.
Relacje. Relacja oznacza określony związek między obiektami
jakiegoś typu. Przykładowo niech ![]() oznacza zbiór mężczyzn,
zaś
oznacza zbiór mężczyzn,
zaś ![]() zbiór kobiet. Na
zbiorach tym rozważamy relację
zbiór kobiet. Na
zbiorach tym rozważamy relację ![]() bycia synem, tzn. fakt, że
mężczyzna
bycia synem, tzn. fakt, że
mężczyzna ![]() i kobieta
i kobieta ![]() są w relacji
są w relacji ![]() oznacza dokładnie,
że
oznacza dokładnie,
że ![]() jest synem
jest synem ![]() .
Zwróćmy uwagę, że relacja
.
Zwróćmy uwagę, że relacja ![]() jest w pełni opisana przez zbiór
jest w pełni opisana przez zbiór
Zwróćmy uwagę, że każdy ze sposobów 1-3 z definicji 7.4
jest symbolicznym sposobem zapisu funkcji zdaniowej ``![]() i
i ![]() są w
relacji
są w
relacji ![]() '', gdzie zakres
'', gdzie zakres ![]() to
to ![]() , zaś zakres
, zaś zakres ![]() to
to
![]() . Relacja
. Relacja ![]() , jako podzbiór produktu
, jako podzbiór produktu ![]() , jest natomiast
wykresem tej funkcji zdaniowej. W ten sposób dostajemy mnóstwo
przykładów funkcji zdaniowych.
, jest natomiast
wykresem tej funkcji zdaniowej. W ten sposób dostajemy mnóstwo
przykładów funkcji zdaniowych.
W definicji 7.4 wprowadziliśmy pojęcie relacji
dwuargumentowej (binarnej). Rozważa się również relacje o innej
liczbie argumentów. Mianowicie, dla ![]() relacja
relacja ![]() -argumentowa
na zbiorach
-argumentowa
na zbiorach ![]() to dowolny podzbiór
to dowolny podzbiór ![]() produktu
kartezjańskiego
produktu
kartezjańskiego
![]() . Dla
. Dla ![]() relację
relację ![]() nazywamy też relacją unarną. W przypadku, gdy
nazywamy też relacją unarną. W przypadku, gdy
W przypadku relacji binarnej ![]() na zbiorach
na zbiorach ![]() i
i ![]() definiujemy
dziedzinę i obraz relacji
definiujemy
dziedzinę i obraz relacji ![]() jako zbiory
jako zbiory
Definiujemy też relację odwrotną ![]() do relacji
do relacji ![]() wzorem
wzorem
Gdy ![]() jest relacją na zbiorze
jest relacją na zbiorze ![]() oraz
oraz ![]() jest podzbiorem
jest podzbiorem ![]() , to
definiujemy ograniczenie (obcięcie) relacji
, to
definiujemy ograniczenie (obcięcie) relacji ![]() do zbioru
do zbioru ![]() wzorem
wzorem
W przypadku relacji ![]() na zbiorach skończonych
na zbiorach skończonych ![]() wygodnie jest
przedstawiać ją graficznie w postaci diagramu. Strzałka od
wygodnie jest
przedstawiać ją graficznie w postaci diagramu. Strzałka od ![]() do
do
![]() oznacza
oznacza ![]() .
.
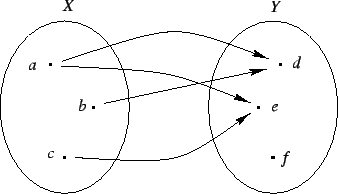
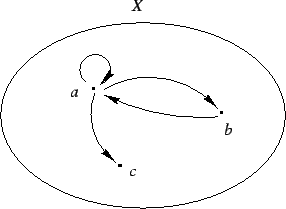
2. Relacja porządku ![]() na zbiorze liczb rzeczywistych.
na zbiorze liczb rzeczywistych.
3. Relacja równoległości
![]() na zbiorze prostych
na zbiorze prostych ![]() na płaszczyźnie.
na płaszczyźnie.
4. Relacja podzielności ![]() na zbiorze liczb naturalnych
na zbiorze liczb naturalnych
![]() .
.
5. Relacja inkluzji ![]() na zbiorze potęgowym
na zbiorze potęgowym ![]() dla ustalonego zbioru
dla ustalonego zbioru ![]() .
.
Jak już wspomnieliśmy, relacji można używać do definiowania
funkcji zdaniowych wskazujących, że pewne formuły nie są
tautologiami.
Przykładowo zrobimy to dla formuły
Rozważa się różne własności relacji ![]() na zbiorze
na zbiorze ![]() .
.
Jako ćwiczenie pozostawiamy stwierdzenie, jak przy pomocy diagramu
relacji ![]() rozpoznać powyższe własności.
rozpoznać powyższe własności.
W powyższych przykładach relacji, relacja pusta ![]() jest
przechodnia, symetryczna, antysymetryczna, lecz nie jest zwrotna ani
spójna (na niepustym zbiorze
jest
przechodnia, symetryczna, antysymetryczna, lecz nie jest zwrotna ani
spójna (na niepustym zbiorze ![]() ).
).
Relacja ![]() na zbiorze
na zbiorze ![]() jest zwrotna, przechodnia,
antysymetryczna i spójna.
jest zwrotna, przechodnia,
antysymetryczna i spójna.
Relacja równoległości na zbiorze prostych na płaszczyźnie ![]() jest zwrotna, symetryczna i przechodnia, lecz nie jest antysymetryczna
ani spójna.
jest zwrotna, symetryczna i przechodnia, lecz nie jest antysymetryczna
ani spójna.
Relacja podzielności na zbiorze ![]() jest zwrotna, przechodnia,
antysymetryczna, lecz nie jest symetryczna ani spójna.
jest zwrotna, przechodnia,
antysymetryczna, lecz nie jest symetryczna ani spójna.
Relacja inkluzji na zbiorze ![]() jest zwrotna, przechodnia,
antysymetryczna, lecz nie jest spójna ani symetryczna (gdy
jest zwrotna, przechodnia,
antysymetryczna, lecz nie jest spójna ani symetryczna (gdy ![]() ma
więcej niż jeden element).
ma
więcej niż jeden element).
W następnych dwóch rozdziałach poznamy najważniejsze rodzaje relacji: relacje porządkujące i relacje równoważności.
Ludomir Newelski 2006-08-29