THE AREA OF A SPECTRALLY POSITIVE STABLE PROCESS STOPPED
AT ZERO
Julien Letemplier
Thomas Simon
Abstract: A multiplicative identity in law for the area of a spectrally positive Lévy 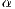 -stable
process stopped at zero is established. Extending that of Lefebvre for Brownian motion, it
involves an inverse beta random variable and the square of a positive stable random variable.
This simple identity makes it possible to study precisely the behaviour of the density at zero,
which is Fréchet-like.
-stable
process stopped at zero is established. Extending that of Lefebvre for Brownian motion, it
involves an inverse beta random variable and the square of a positive stable random variable.
This simple identity makes it possible to study precisely the behaviour of the density at zero,
which is Fréchet-like.
2010 AMS Mathematics Subject Classification: Primary: 60G52; Secondary: 60E07,
60G51.
Keywords and phrases: Hitting time, integrated process, stable Lévy process, tail
asymptotics.