BESSEL POTENTIALS, GREEN FUNCTIONS AND EXPONENTIAL
FUNCTIONALS ON HALF-SPACES
T. Byczkowski
M. Ryznar
H. Byczkowska
Abstract: The purpose of the paper is to provide precise estimates for the Green function
corresponding to the operator 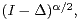
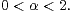 The potential theory of this
operator is based on Bessel potentials
The potential theory of this
operator is based on Bessel potentials 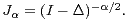 In probabilistic terms it
corresponds to a subprobabilistic process obtained from the so-called relativistic
In probabilistic terms it
corresponds to a subprobabilistic process obtained from the so-called relativistic 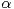 -stable
process. We are interested in the theory of the killed process when exiting a fixed half-space.
The crucial role in our research is played by (recently found) an explicit form of the Green
function of a half-space. We also examine properties of some exponential functionals
corresponding to the operator
-stable
process. We are interested in the theory of the killed process when exiting a fixed half-space.
The crucial role in our research is played by (recently found) an explicit form of the Green
function of a half-space. We also examine properties of some exponential functionals
corresponding to the operator 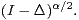
2000 AMS Mathematics Subject Classification: Primary 60J65; Secondary 60J60.
Key words and phrases: Bessel potentials, Riesz kernels, relativistic process, stable
process, Poisson kernel, Green function, half-spaces.