UNIVERSITY
OF WROCŁAW
 
Main Page
Contents
Online First
General Information
Instructions for authors


VOLUMES
44.1 43.2 43.1 42.2 42.1 41.2 41.1
40.2 40.1 39.2 39.1 38.2 38.1 37.2
37.1 36.2 36.1 35.2 35.1 34.2 34.1
33.2 33.1 32.2 32.1 31.2 31.1 30.2
30.1 29.2 29.1 28.2 28.1 27.2 27.1
26.2 26.1 25.2 25.1 24.2 24.1 23.2
23.1 22.2 22.1 21.2 21.1 20.2 20.1
19.2 19.1 18.2 18.1 17.2 17.1 16.2
16.1 15 14.2 14.1 13.2 13.1 12.2
12.1 11.2 11.1 10.2 10.1 9.2 9.1
8 7.2 7.1 6.2 6.1 5.2 5.1
4.2 4.1 3.2 3.1 2.2 2.1 1.2
1.1
 
 
WROCŁAW UNIVERSITY
OF SCIENCE AND
TECHNOLOGY

Contents of PMS, Vol. 26, Fasc. 1,
pages 121 - 142
 

MINIMAL INTEGRAL REPRESENTATIONS OF STABLE PROCESSES

Jan Rosiński

Abstract: Minimal integral representations are defined for general stochastic processes and completely characterized for stable processes (symmetric and asymmetric). In the stable case, minimal representations are described by rigid subsets of the 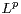Lp -spaces which are investigated here in detail. Exploiting this relationship, various tests for the minimality of representations of stable processes are obtained and used to verify this property for many representations of processes of interest.

2000 AMS Mathematics Subject Classification: Primary: 60G07, 60G57; Secondary: 60E07, 60G25.

Key words and phrases: Stable processes, stochastic integral representations, isometries on 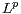Lp -spaces.

Download:    Abstract    Full text   Abstract + References