OCCUPATION TIME FLUCTUATIONS OF POISSON AND EQUILIBRIUM
BRANCHING SYSTEMS IN CRITICAL AND LARGE DIMENSIONS
Abstract: Limit theorems are presented for the rescaled occupation time fluctuation process of a
critical finite variance branching particle system in 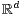 with symmetric
with symmetric 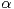 -stable motion
starting off from either a standard Poisson random field or the equilibrium distribution for
critical
-stable motion
starting off from either a standard Poisson random field or the equilibrium distribution for
critical 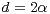 and large
and large 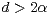 dimensions. The limit processes are generalised Wiener
processes. The obtained convergence is in space-time and finite-dimensional distributions
sense. Under the additional assumption on the branching law we obtain functional
convergence.
dimensions. The limit processes are generalised Wiener
processes. The obtained convergence is in space-time and finite-dimensional distributions
sense. Under the additional assumption on the branching law we obtain functional
convergence.
2000 AMS Mathematics Subject Classification: Primary: 60F17, 60G20; Secondary:
60G15.
Keywords and phrases: Functional central limit theorem; occupation time
fluctuations; branching particles systems; generalised Wiener process; equilibrium
distribution.