ASYMPTOTIC BEHAVIOR OF ULTIMATELY CONTRACTIVE ITERATED
RANDOM LIPSCHITZ FUNCTIONS
Gerold Alsmeyer
Gerd Hölker
Abstract: Let 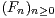 be a random sequence of i.i.d. global Lipschitz functions on a complete
separable metric space
be a random sequence of i.i.d. global Lipschitz functions on a complete
separable metric space 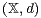 with Lipschitz constants
with Lipschitz constants 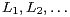 For
For 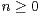 , denote by
, denote by
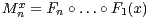 and
and 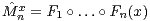 the associated sequences of forward
and backward iterations, respectively. If
the associated sequences of forward
and backward iterations, respectively. If 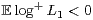 (mean contraction) and
(mean contraction) and
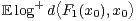 is finite for some
is finite for some 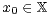 , then it is known (see [9]) that, for each
, then it is known (see [9]) that, for each
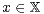 , the Markov chain
, the Markov chain 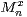 converges weakly to its unique stationary distribution
converges weakly to its unique stationary distribution 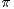 ,
while
,
while 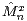 is a.s. convergent to a random variable
is a.s. convergent to a random variable 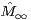 which does not depend on
which does not depend on 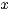 and has distribution
and has distribution 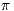 . In [2], renewal theoretic methods have been successfully
employed to provide convergence rate results for
. In [2], renewal theoretic methods have been successfully
employed to provide convergence rate results for 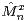 , which then also lead to
corresponding assertions for
, which then also lead to
corresponding assertions for 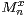 via
via 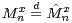 for all
for all 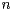 and
and 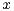 , where
, where 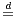 means equality in law. Here our purpose is to demonstrate how these methods are
extended to the more general situation where only ultimate contraction, i.e. an
a.s. negative Lyapunov exponent
means equality in law. Here our purpose is to demonstrate how these methods are
extended to the more general situation where only ultimate contraction, i.e. an
a.s. negative Lyapunov exponent 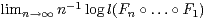 is assumed (here
is assumed (here
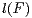 denotes the Lipschitz constant of
denotes the Lipschitz constant of 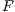 ). This not only leads to an extension of
the results from [2] but in fact also to improvements of the obtained convergence
rate.
). This not only leads to an extension of
the results from [2] but in fact also to improvements of the obtained convergence
rate.
2000 AMS Mathematics Subject Classification: Primary: 60J05; Secondary: 60K05,
60G17.
Keywords and phrases: Random Lipschitz function, ultimately contractive, forward
iterations, backward iterations, stationary distribution, Prokhorov metric, level 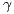 ladder
epochs, Lyapunov exponent.
ladder
epochs, Lyapunov exponent.