ON A BAHADUR–KIEFER REPRESENTATION OF VON MISES STATISTIC
TYPE FOR INTERMEDIATE SAMPLE QUANTILES
Nadezhda Gribkova
Roelof Helmers
Abstract: We investigate a Bahadur–Kiefer type representation for the 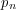 -th empirical quantile
corresponding to a sample of
-th empirical quantile
corresponding to a sample of  i.i.d. random variables when
i.i.d. random variables when 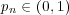 is a sequence
which, in particular, may tend to zero or one, i.e., we consider the case of intermediate sample
quantiles. We obtain an ‘in probability’ version of the Bahadur–Kiefer type representation
for a
is a sequence
which, in particular, may tend to zero or one, i.e., we consider the case of intermediate sample
quantiles. We obtain an ‘in probability’ version of the Bahadur–Kiefer type representation
for a 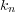 -th order statistic when
-th order statistic when 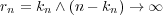 ,
, 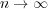 , without any
restrictions of the rate at which
, without any
restrictions of the rate at which 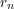 tends to infinity. We give a bound for the remainder term
in the representation with probability
tends to infinity. We give a bound for the remainder term
in the representation with probability 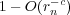 for arbitrary
for arbitrary 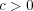 . We obtain also
an ‘almost sure’ version under the additional assumption that
. We obtain also
an ‘almost sure’ version under the additional assumption that 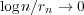 as
as
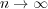 .
.
Finally, we establish a Bahadur–Kiefer type representation for the sum of order statistics
lying between the population 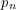 -quantile and the corresponding intermediate sample
quantile by a von Mises type statistic approximation, especially useful in establishing second
order approximations for slightly trimmed sums.
-quantile and the corresponding intermediate sample
quantile by a von Mises type statistic approximation, especially useful in establishing second
order approximations for slightly trimmed sums.
2000 AMS Mathematics Subject Classification: Primary: 62G30, 62G32; Secondary:
62G20, 62E20.
Keywords and phrases: Bahadur–Kiefer type representation, intermediate sample
quantiles, Bahadur–Kiefer processes, empirical processes, quantile processes, von Mises
statistic type approximation, slightly trimmed sum.