Opracowania dotyczące wielościanów i tożsamości Eulera

W tym dziale znajdziecie następujące opracowania.

     [W1] "O pryzmatoidach i tożsamości Eulera" autorstwa Ingi Skowrońskiej.
     [W2] "Ilości wierzchołków, krawędzi i ścian w wielościanach wypukłych" autorstwa Urszuli Karbowskiej.
     [W3] "Graniastosłupy skręcone" autorstwa Barbary Kuźnar.
     [W4] "Równoważność przez rozkład dla graniastosłupów" autorstwa Beaty Zwierzańskiej.
     [W5] "O pewnym sposobie ścisłego wprowadzenia pojęcia pola wielokątów i objętości wielościanów" autorstwa Magdaleny Dukiewicz.

Poniżej zamieszczam nieco obszerniejsze omówienia prac z tego działu.

[W1] Nietrudny dowód wzoru Eulera dla wielościanów wypukłych z wykorzystaniem własności brył zwanych pryzmatoidami

Inga Skowrońska, "O pryzmatoidach i tożsamości Eulera", praca magisterska, 2001. plik pdf

Wzór Eulera to związek pomiędzy ilościami wierzchołków (W), krawędzi (K) i ścian (S) w dowolnym wielościanie wypukłym.
Ma on następującą postać: W-K+S=2.
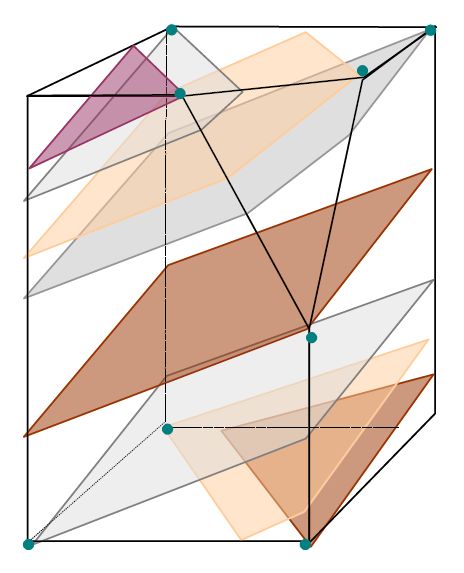
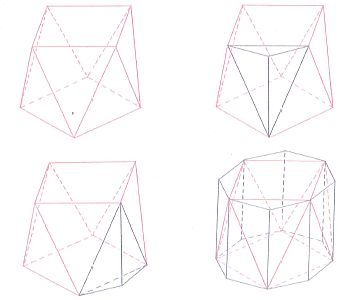
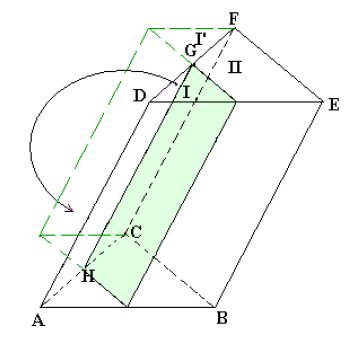
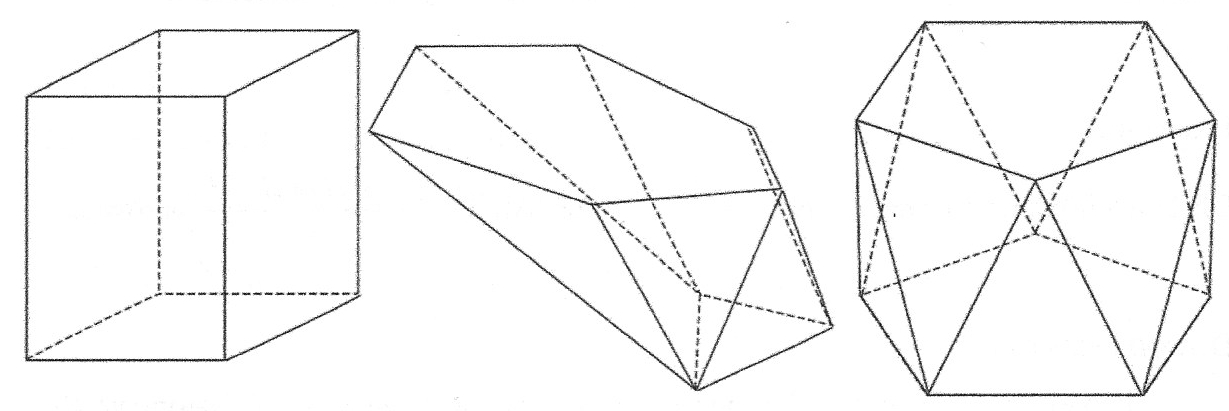
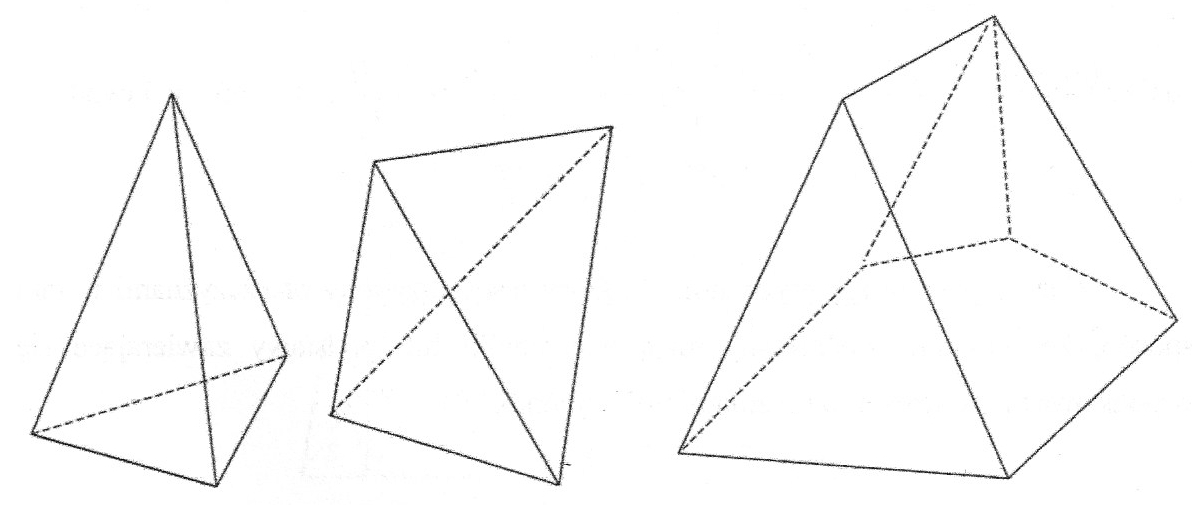
Pryzmatoidy to rodzina brył obejmująca między innymi wszystkie graniastosłupy i ostrosłupy, a także wiele innych brył. Łączy je to, że są wielościanami wypukłymi, których wszystkie wierzchołki znajdują się na dwóch poziomach (na dwóch równoległych płaszczyznach).
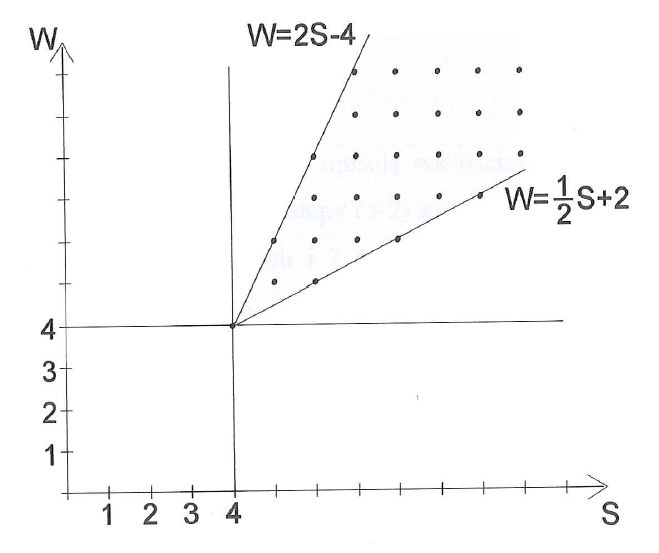
Uzasadnienie, że wzór Eulera zachodzi dla wszystkich pryzmatoidów jest bardzo proste. W pracy wyjaśnione jest jak można wykorzystać ten fakt, i to że każdy wypukły wielościan daje się rozciąć na pryzmatoidy, do uzasadnienia wzoru Eulera dla wszystkich wielościanów wypukłych.

[W2] Jakie trójki liczb W,S,K pojawiają się jako liczby wierzchołków, ścian i krawędzi (odpowiednio) w wielościanach wypukłych?

Urszula Karbowska, "Ilości wierzchołków, krawędzi i ścian w wielościanach wypukłych", praca magisterska, 2002. plik pdf

Chyba każdy od razu przyzna, że ilość ścian w wielościanie wypukłym może być dowolną liczbą od 4 w górę. A jak ustalimy liczbę S ścian, to jaki zakres wartości może przebiegać liczba wierzchołków w wielościanach o tylu ścianach? To już jest mniej oczywiste. Można wreszcie zapytać, jakie trójki liczb tworzą zakres dla możliwej ilości ścian, wierzchołków i krawędzi w wielościanach wypukłych. To właśnie pytanie, i znalezienie na nie pełnej odpowiedzi, jest głównym tematem zaprezentowanej tu pracy.

Diagram obok przedstawia (za pomocą punktów w układzie kartezjańskim) zakres par liczb W,S występujących jako ilości wierzchołków i ścian w wielościanach wypukłych. W każdym z tych przypadków liczbę krawędzi wyznacza się z tożsamości Eulera, jako K=W+S-2. Więcej szczegółów znajdziecie w tekscie pracy.

[W3] Graniastosłupy skręcone bez tajemnic

Barbara Kuźnar, "Graniastosłupy skręcone", praca magisterska, 2002. plik pdf

Mało znaną a ciekawą rodzinę brył stanowią tzw. graniastosłupy skręcone (zwane też czasem antygraniastosłupami). Prezentowana tu bardzo przystępna praca zawiera opis tych brył, oraz ich wszechstronną analizę pod kontem "szkolnych" własności, takich jak:
• wyprowadzenie wzorów na objętość oraz pole powierzchni,
• analizę możliwości wpisania i opisania kuli, oraz wyznaczenie ich promieni,
• znalezienie wszystkich symetrii własnych takich brył,
• wyznaczenie parametrów, dla których graniastosłup skręcony staje się bryłą archimedesową,
i innych.

Rysunek obok ilustruje podejście do obliczenia objętości granaistosłupa skręconego, opisane i omówione dokładniej w pracy. Graniastosłup skręcony (czworokątny) to bryła w lewej górnej części rysunku.

[W4] Czy dowolne dwa graniastosłupy o tej samej objętości można rozciąć tak, by otrzymać z nich jednakowe kolekcje części?

Beata Zwierzańska, "Równoważność przez rozkład dla graniastosłupów", praca magisterska, 2006. plik pdf

Zjawisko polegające na tyum, że jedna bryła daje się rozciąć na części, z których można złożyć drugą bryłę nazywa się równoważnością przez rozkład. Bryły równoważne przez rozkład muszą oczywiście mieć jednakowe objętości. Pytanie, czy każde dwa wielościany o tej samej objętości są równoważne przez rozkład jest trudne, ale okazuje się, że tak być nie musi. Na przykład, czworościan foremny i sześcian o jednakowych objętościach nie są równoważne przez rozkład. Tymczasem jeśli ograniczymy się do graniastosłupów, ale nie tylko prostych lecz również pochyłych, odpowiedź na powyższe pytanie nie jest taka trudna, i jest pozytywna, co zostało wyjaśnione w zamieszczonej tu pracy.

Rysunek obok ilustruje fakt równoważności przez rozkład graniastosłupa trójkątnego z pewnym równoległościanem.

[W5] Jak ściśle powiedzieć czym jest objętość wielościanów?

Magdalena Dukiewicz, "O pewnym sposobie ścisłego wprowadzenia pojęcia pola wielokątów i objętości wielościanów", praca magisterska, 2005. plik pdf

Jak wyznaczyć objętość dowolnego wielościanu? Podzielić go na czworościany, i zsumować ich objętości wyliczone ze wzoru V=Sh/3. A skąd pewność, że wynik nie zależy od sposobu podziału? O tym właśnie jest ta praca!
Uzasadnienie tego faktu nie jest zbyt proste, ale daje się przedstawić w sposób elementarny. Wykorzystuje się w nim, podobnie jak w pracy [W1], możliwość podziału dowolnego wielościanu na bryły zwane pryzmatoidami.

Rysunek obok przedstawia kilka przykładowych pryzmatoidów, oraz uniwersalny wzór na objętość dla wszystkich pryzmatoidów. Wzór ten także odgrywa ważną rolę w uzasadnieniu głównej tezy pracy. W tym wzorze S₁ oznacza pole podstawy górnej (które może być zerowe gdy ta podstawa jest zredukowana do krawędzi lub wierzchołka), S₂ oznacza pole podstawy dolnej (także może wynosić 0), D oznacza pole przekroju bryły w połowie wysokości, zaś h oznacza wysokość. Po dalsze szczegóły i wyjaśnienia zapraszam do tekstu pracy, do Rozdziału 3. Rozdziały 1 i 2 mogą być potraktowane jako "rozgrzewka", i dotyczą pojęcia pola dla wielokątów.