Literatura:
- C.L. Evans An Introduction to Mathematical Optimal Control Theory
- M. Lachowicz Teoria sterowania
- P. Pedregal Introduction to Optimization
Zagadnienia:
- Minimalizacja funkcji liniowych (sympleks) oraz nieliniowych (mnożniki)
- Punkty krytyczne funkcjonałów (będzie kontynuowane...)
Tematy
- SIR
- Epidemia
- Zombie
- SHJB
- Szybowiec
- Koronawirus
- Rynek
- Powierzchnie
- Zabezpieczenia
- Żuki
- Auta
Wykład oraz ćwiczenia:
- Optymalizacja w pdf.
- Euler-Lagrange czat 16 III 2020r.
- Euler-Lagrange quiz 16 II 2020r.
- Lagrange multipliers czat 23 III 2020r.
- Lagrange multipliers quiz 23 II 2020r.
Programowanie matematyczne i optymalizacja.
Zadanie 0. Metodą sympleks i geometryczną znaleźć min i max o ile to możliwe funkcji $f(x_1,x_2)=3x_1-x_2$ w nieujemnej ćwiartce, gdzie $x_1+x_2\le 8$, $x_2-x_1\le 1$ oraz $x_1-2x_2\le 2$. Więcej zadań w pliku por.pdf.
Zadanie 1. Oblicz inf/min funkcji $f(x,y)=xy$ oraz $f(x,y)=x^2+y^2$ na zbiorach $[-1,1]^2$ oraz $\mathbb{R}^2$.
Użyj wolphramalpha.com do wizualizacji.
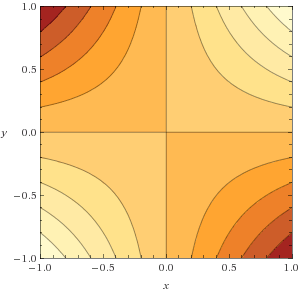
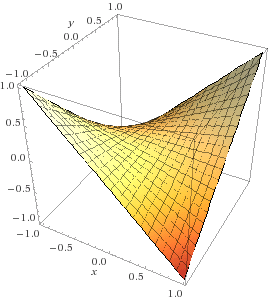
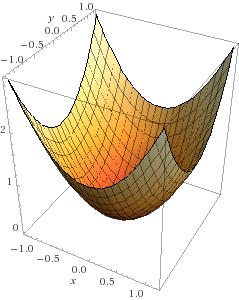
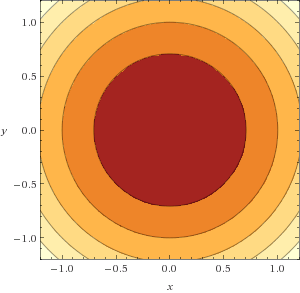
Zadanie 2. Wyznaczyć min i max funkcji $f(x,y)=3x-y$ na zbiorze $$\{(x,y)\in \mathbb{R}_+^2:x+y\le 8, y-x\le 1, x-2y\le 2\}.$$ Zastosuj metodę bezpośrednią oraz algorytm sympleks.
Zadanie 3. Metodą sympleks, analityczną i geometryczną znaleźć min i max funkcji $f(x,y,z)=x+y+z$ na podzbiorze $2x+y+2z \le 4$ nieujemnej ósemki.
Zadanie 4. Znaleźć ekstrema funkcji $f(x,y)=xy\ \ \ {\rm z\ warunkiem}\ \ \ x^2+y^2=1.$
Zadanie 5. Przeanalizuj punkty krytyczne następujących funkcji $$f(x,y)=x^2-y^2,\; f(x,y)=xy,\; f(x,y)=x^4+y^4-4xy,\; f(x,y)=(x^2-y^2-a)e^{-x^2-y^2}\,$$ na płaszczyźnie, kole, okręgu, kwadracie oraz jego brzegu.
Zadanie 6. Znaleźć ekstrema funkcji $4x+3y$ z warunkiem $x^2+y^2=1$, a następnie funkcji $x^2+y^2$ z warunkiem $3x+4y=1$.
Zadanie 7. Prześledzić zagadnienia dotyczące punktów krytycznych funkcjonałów z monografii: Marka Kota oraz autorstwa: Butazzo, Giaquinta, Hildebrandt. Cytowane monografie: Calculus of Variations oraz 1D Variational Problems.
Zadanie 8. Metoda sympleks, wg: Porazińskiej lub Pedregala.
Zadanie 9. Obliczyć posiłkując się wykładem równanie Eulera-Lagrange'a dla funkcjonału $$J(u)=\int_\Omega \sqrt{1+u_x^2+u_y^2} dxdy\,.$$
Zadanie 10. Obliczyć max i min funkcji $f=z$ przy ograniczeniu $x+2+y^2+z^2=1$ (a następnie $x^2+y^2+z^2=1$ przy tej samej $f=z$), podobnie przeanalizować przypadek dwuwymiarowy.
Zadanie 11. Wybierz i rozwiąż zadanie ze źródeł: Lagrange multipliers @Harvard, @Ediburgh, Kot.pdf.
Zadanie 12. Sformułuj i rozwiąż równanie Eulera-Lagrange'a z $u(0)=u(1)=0$ dla funkcjonału $$J(u)=\int_0^1 a u^2+ b u'^2=\int_0^1 a (u(x))^2+ b (u'(x))^2 dx$$ w zależności od parametrów rzeczywistych $a$ i $b$, dla jakich wartości punkt krytyczny jest typu minimum. Rozważ wybrane ustalone wartości $a$ i $b$ jeśli pełna ogólność stanowi problem, a następnie zmień je i porównaj, najlepiej przyjąć dwie różne pary tak aby raz osiągnąć minimum, a raz inny punkt krytyczny. Jakie różnice pojawiają się, gdy $u(0)=A$ i $u(1)=B$. O $u$ zakładamy np. $C^1$ bądź $H^1$, czyli pochodna $u'$ jest albo ciągła, albo całkowalna z kwadratem.
Zadanie 13. Sformułuj i rozwiąż równanie Eulera-Lagrange'a z $u(0)=u(1)=0$ dla funkcjonału $J(u)=\int_0^1 a u^2+ b u'^2$ przy ograniczeniu $I(u)=\int_0^1 c (u(x))^2+ d (u'(x))^2 dx=1$ dobierając stałe tak jak ci pasuje, ale z trywialnością bez przesady.
Zadanie 14. Wybierz i opracuj któryś z przykładów: na str. 16 mnożniki Lagrange'a w wersji bez całki Calculus of Variations, na str. 46 przykład calkowych więzów One dimensional..., ze str. 16 z wykładu 5 z notatek optymalizacja.pdf a także sformułuj na istnienie minimum warunki dostateczne.
Zadanie 15. Dla jakich wartości parametru $a$ i $p$ funkcjonał $$J(u)=\int_0^1 u'(x)^2+au(x)^p dx$$ jest dobrze określony; ograniczony z dołu; wypukły; koercytywny; ciągły; różniczkowalny na: $H^1$ lub $C^1$ z zerowymi warunkami brzegowymi. Kiedy posiada minimum? Wybierz ustalone parametry.
Zadanie 16. Opracuj wybrane zagadnienie z książki Mawhina o Metodach Wariacyjnych.
Zadanie 17. Mnożniki Lagrange'a dla funkcjonału $$J(u)=\int_0^1 u'(x)^2+au(x)^p dx$$ z ograniczeniem $\int_0^1 u(x)^r dx=1$ oraz $u(0)=u(1)=0$ dla wybranych $a$ i $p, r$. Wsk. na czacie rozważaliśmy $p=4$ oraz $r=2$. Rozwiązanie równania Eulera-Lagrange'a przy pomocy geometrycznej metody jest tutaj.
Zadanie 18. Używając mnożników Lagrange'a znajdź punkty krytyczne funkcjonału $$J(u)=\int_0^1 u'(x)^2 dx$$ na przestrzeni funkcji $u(0)=u(1)=0$ spełniających $\int_0^1 u(x) dx=1$.
Zadanie 19. Używając mnożników Lagrange'a znajdź punkty krytyczne funkcjonału $$J(u)=\int_0^2 u(x)\sqrt{u'(x)^2+1} dx$$ na przestrzeni funkcji $u(0)=u(2)=0$ spełniających $\int_0^2 \sqrt{u'(x)^2+1} dx=1$. Wsk. użyj równania Eulera-Lagrange'a w wersji Beltramiego dla skojarzonego funkcjonału Lagrange'a $L$. Jaką interpretację posiada to zadanie?
Zadanie 20. Zmaksymalizuj pole $$\int_a^b u(x) dx$$ przy zadanej długości krzywej $\int_a^b \sqrt{u'(x)^2+1} dx=L$ z warunkami $u(a)=A$ i $u(b)=B$. Zamiast ogólnych rozważań zacznij od przypadku półokręgu o promieniu $1$ i środku $x=0=u$. Ile wówczas wynoszą dane $A,B,L,a,b$, bo rozwiązanie już mamy, tylko zadania brak.
Zadanie 21. Regresja liniowa i logistyczna (mnożnikami Lagrange'a) z wykładu 14 z pliku optimization.pdf minimalizujące odchylenie standardowe, jego kwadrat, przy równych wartościach średnich.
Zadanie 22. Zilustruj tezę twierdzenia o przełęczy górskiej przykładem $f(x,y)=x^2-y^2$ lub $f(x,y)=x^4-y^4$. Czy teza zachodzi? Czy założenia są spełnione? Czy można skorzystać z twierdzenia?
Zadanie 23. Przeanalizuj przykład piekielnych wrót, czyli $f(x,y)=x^4 (y-\sin(1/x))^2$ w świetle tezy twierdzenia o przełęczy górskiej. Czy istnieje krzywa realizująca min?
Zadanie 24. Znajdź przełęcz górską dla przykładowej funkcji $f(,xy)=(x^2-y^2-0.2)\exp (-x^2-y^2)\,.$
Zadanie 25. Znajdź przełęcz górską dla funkcji $f(x,y)=(x^2-y^2)\exp (x^4+y^4-4x^2-4y^2)\,.$
Zadanie 26. Przełęcz górska dla $f(x,y)=x^2+(1-x)^3y^2$ por. Analiza Nieliniowa aut. W. Kryszewskiego.
Zadanie 27. Wykazać dla $J(u)=\int_0^1u'(x)^2 - u(x)^4 dx$ mamy $J(tsin(\pi \cdot))<0$, gdy $t$ dostatecznie duże. Obliczyć dokładną wartość $J(tsin)$.Na ile można uogólnić powyższe rozumowanie zastępując potęgę $4$ na inną większą niż $2$. Udowodnić warunek Palais-Smale'a na $H_0^1$ czyli $u(0)=u(1)=0$, a $u,u'$ w $L^2$.
Zadanie 28. Obliczyć max i min funkcji $f=(x^2-y^2)\exp(-x^2-y^2)$ oraz zbadać strukturę przełęczy górskiej w świetle twierdzeń Ambrosettiego-Rabinowitza oraz Couranta, pokazać podobieństwa i różnice.
Zadanie 29. Wykazać nierówność $\int_0^1 u(x)^2 dx \le \int_0^1 u'(x)^2 dx$, czy można ją poprawić dopisująć współczynnik mniejszy od $1$, dla $u(0)=u(1)=0$? Zminimalizuj funkcjonał $\int_0^1 u(x)^2 dx / \int_0^1 u'(x)^2 dx$ po $u(0)=u(1)=0$.
Zadanie 30. Rozważmy równanie $x'(t)=a(t)x(t)$ oraz funkcjonał $$P(a)=\int_0^T x(t)(a(t)-C) dt$$ gdzie $a(t)\in [A,B]$. Dobierz sobie stałe $A,B,C$ unikatowe, inne niż na czacie. Ustal $x_0=x(0)$ dobrane do danych, podobnie $T$ aby rachunki były dość łatwe. Dla funkcji stałych $a$ równych $A$ oraz $B$ oblicz wartości funkcjonału $P$. Zbadaj monotoniczność $P$ względem stałych $a$. Zastosuj ZMP do maksymalizacji $P$. Porównaj uzyskaną optymalną wartość $P$ dla $a$ z ZMP, z wartościami $P$ dla $a=A$ oraz $a=B$. Rozważ funkcję schodkową o wartościach $A$ i $B$ z przełączeniem w punkcie $s$. Wylicz bezpośrednio bez ZMP maksimum $P$ od tej funkcji schodkowej w zależności od zmiennej $s$. Czy uzyskano taką samą wartość $S$ jak z ZMP?
Zadanie 31. Rozwiązać dowolne zadanie ze str 74 monografii M. Lachowicza.
Zadanie 32. Rozważmy równanie $x'(t)=rx(t)-a(t)m$ harmonijnej spłaty pożyczki $x(t)$ oraz funkcjonał minus-kosztu $$P(a)=-\int_0^T a(t) dt-x(T)$$ gdzie $a(t)\in [0,1]$. Rozważyć parametry $e^{rT}=1$ oraz $m>1$, np. $m=2$ lub $m={\rm e}=\exp(1)$. Warunek początkowy $x(0)=x_0$. Co w przypadku, gdy $m<1$, rozważyć $m=1/2$ np.
Zadanie 33. Rozważmy równanie $x'=-x+a$ wraz z funkcjonałem $P=\int_0^1 x^2+a^2$, który chcemy zminimalizować oraz warunkiem $x(0)=1$.
Zadanie 34. Uzupełnić pozostałe dwa przypadki (oprócz sterowania z przełączeniem, mamy dwa inne sterowania optymalne bez przełączeń, w zależności od wartości $mx(T)^2$) dla zadania z czatu $x'=ix-am$ z funkcjonałem maksymalizowanym $P=-1/3 x(T)^3-\int_0^T a^2$ gdzie $x(0)=x_0$, $i>1$, $m>0$. Dobrać sobie dane tak by rachunki były możliwie najprostsze.
Zadanie 35. Policzyć ZMP równania $x'=x+a$ dla minimum z $P=x(T)^2+\int a^2$ jak na czacie. Przyjąć wygodne stałe, np. T>0. Porównaj z $a=0$, czyli bezczynnością.
Zadanie 36. Wybrać dowolne kwadratowe lub nieliniowe zagadnienie z ZMP z Evansa, Pedregala czy Lachowicza.
